Solved: Da Vinci’s 500-year-old mystery about bubbles

Pour water — or another tasty, bubbly liquid — into a clear glass. Carefully watch bubbles as they nucleate and then float up in the glass: You’ll notice that some of them rise differently than others. The tiniest ones shoot straight up, while bigger bubbles rhythmically bounce back and forth, slowing their trip. If you’ve ever wondered why this occurs, you’re not alone. No less a natural philosopher than Leonardo da Vinci was confounded by it.

Bubble, bubble, toil and trouble

Kids are fascinated by bubbles, and apparently so are some scientists, one of whom described them this way: “Bubbles are emptiness, non-liquid, a tiny cloud shielding a mathematical singularity. Born from chance, a violent and brief life ending in the union with the (nearly) infinite.”

In his famous sketchbooks (like the one that depicted a helicopter that finally flew in 2022), da Vinci drew and described the mysterious bubbly phenomenon. Armed with modern theories, the unresolved question caught the eye of 20th century scientists. Their attempts to solve it by hand, and in subsequent decades via computer, were only partially successful. None of them got it quite right.

But now, a mathematical and conceptual answer may finally have been found. A new paper in the journal Proceedings of the National Academy of Sciences describes the solution.

Why bubbles wobble

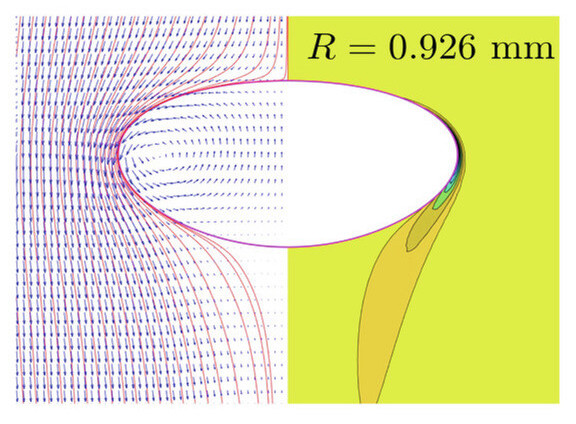
Like all good theoretical work, the paper begins by looking at hard data. Adroit experimental scientists produced a beautiful data set upon which to test theories. Their apparatus emitted air bubbles of precisely determined size into hyper-pure water. Bubbles below a certain radius — roughly 0.91 mm, or just more than 1/32 of an inch — rose straight upward in the water. Above this size, the bubbles began to wobble or spiral about.

Armed with this data, the authors of the new paper built a model to predict bubble behavior. The water and air flow smoothly about one another. When squeezed, these fluids move sideways rather than shrinking. The flow patterns of these incompressible fluids are described by the Navier-Stokes equations, a set of rules laid down in the language of vector calculus. The equations are famously unsolved: There is a $1 million prize for anyone who simply “make[s] substantial progress” on them.

Facing impossible equations, the researchers found clever ways to simplify the math enough to build approximately correct solutions with a computer. The details (which involve terms like non-reflecting boundary conditions, eigenfunctions, and Hopf bifurcation) are far too technical to explain. Suffice it to say, we can use the computer model to explain intuitively why bigger bubbles wobble.

As a spherical bubble rises, it flattens out somewhat, assuming an oval shape with a flat top and rounded bottom. If its spherical diameter is 0.926 mm or more, it is just large enough that a tiny vortex begins to form under its rounded bottom surface. The low pressure of the swirling vortex destabilizes the bubble, causing it to tip to one side.

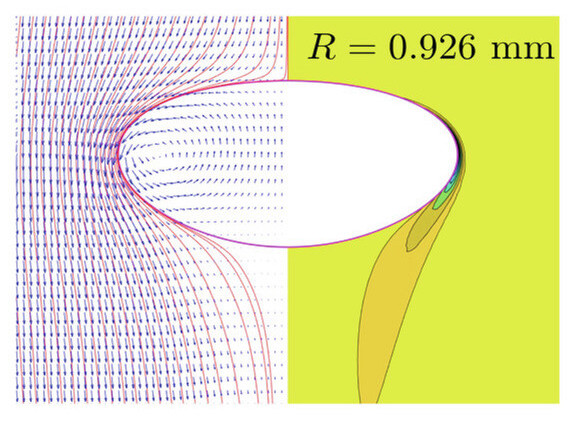
The upward tilted side of the bubble begins to curve more, speeding the motion of the water over the bubble surface on that side. The more quickly flowing water is pressed aside more easily, causing that side of the bubble to rise more quickly. The rapid flow of air on the rising side of the bubble lowers the pressure there, causing the water outside to push it sideways, creating the zig.

Essentially, this is a demonstration of the Bernoulli principle: higher flow velocity creates lower pressure. (You can test this for yourself by placing a piece of very light paper in your palm and blowing over the top. The fast flow of your breath over the top lowers the pressure above the paper, sucking it upward.)

However, the bubble doesn’t zoom away; it zags back again. The sideways zig curves the far side of the bubble. Now that side begins to rise and pull in air, setting up a new low-pressure zone where the water will push back, sending the bubble zagging back in the direction from whence it came.

What’s the point?

A mathematical computer model to explain the rise of water bubbles is arcane. At the same time, it’s another case of scientific progress in the face of the impossible Navier-Stokes equations. Fluid mechanics is the sum of many small victories of this sort. Raise a glass to progress, measured in centuries.